Angulos de elevacion y depresion

ÁNGULO DE ELEVACIÓN: Es el ángulo que se forma entre la visual de un observador que mira hacia arriba y la horizontal
ÁNGULO DE DEPRESIÓN : Es el ángulo que se forma entre la visual de un observador que mira hacia abajo y la horizontal
ver dibujos.

Como se puede observar, en el dibujo de la izquierda, el ave observa hacia abajo al insecto y la horizontal esta a la altura de su vista, por lo tanto el angulo es de depresión. En el dibujo de la derecha el señor, sentado en su silla de ruedas, observa los globos "hacia arriba" por lo tanto el angulo es de elevación.

Para tener en cuenta: En ambos ángulos, la visual del observador será la hipotenusa del triángulo que se forma al plantear una situación problema de este tipo.

Ahora usted esta en capacidad de construir un dibujo con cada situación, diferentes a las presentadas arriba.

Ejemplos de aplicación:

NOTA. En la resolución de triángulos rectángulos vinos qué funciones y procesos utilizar de acuerdo a la información suministrada para su solución. En este tema se aplica la misma situación para resolver los interrogantes.

Ejemplo No 1

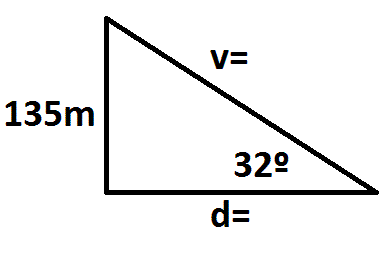
Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto.

(Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión)

Solución.

Observemos la figura.

Se ha generado un triangulo rectángulo, recto en la base del faro. La visual del piloto es la hipotenusa, el ángulo de elevación está formado con la hipotenusa y la horizontal, Luego podemos construir un triangulo auxiliar donde ubicaremos a información suministrada, o si lo prefiere en el mismo dibujo.

Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º  y vamos a buscar el cateto adyacente

Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º

Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales.
Ejemplo 2.
Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual  al otro ángulo alterno interno
La información se muestra en la gráfica.

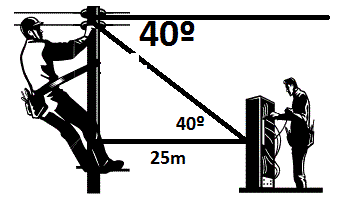
Observemos que el ángulo de depresión se trasladó al interior del triangulo
NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa.
Calculamos con tangente de 40º la altura h  del poste.

Usted está en capacidad de hallar la medida de la visual (v), es decir,  de la hipotenusa. Por favor use la función Coseno de 50º (La respuesta es 32,76 m)

EJERCICIOS
Recuerden que uno de los indicadores de desempeño es: Formular, resolver y argumentar problemas .
Favor mostrar en su, cuaderno, el proceso para llegar a la respuesta correspondiente en cada ejercicio.
1. El piloto de un avión observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la horizontal  del piloto en ese momento es:
A. 9.52 km
B. 8.77 km
C. 11.85m
D. 11.85 km
Pregunta 2: La altura h del piloto  es aproximadamente:
A. 12.85 km
B. 10.67 km
C. 19.67 km
D. 11.93 km
Ejercicio 2. Un navegante ubica (fondea) su barco a 50 m del pie de un faro y observa la torre de éste con un ángulo de elevación de 53°, (ver figura)


Pregunta 3. La altura aproximada del faro:
A. 66,35 m
B. 26, 95 m
C. 16,35 m
D. 12.35 m
Pregunta 4: La longitud aproximada de la visual del barquero es:
A. 90,19 m
B. 83,08 m
C. 53,19 m
D. 24,83 m