Expresiones Algebraicas: 2015

jueves, 12 de noviembre de 2015

Talleres y ejercicios

TALLERES PARA DESCARGAR

Muy Buen día Blogger's , a continuación anexamos diferentes links de talleres y ejercicios que esperamos les sirva para practicar en su tiempo libre ya que la practica hace al maestros y si se les dificulta un poco el tema los invitamos a que sigan intentándolo y pregunten o consulten vídeos que son de mucha ayuda.

Taller 6 Razones Trigonométricas
Taller 7 Aplicaciones Trigonométricas
Taller 8 Ley del Seno y Coseno
Taller 9 Razones Trigonométricas ángulos notables
Taller 10 Ángulos de Referencia
Taller 11 RazonesTrigonométricas con Ángulos negativos
Taller 12 Gráficas de Funciones Trigonométricas
Taller 13 Transformaciones Trigonométricas
Taller 14 Identidades Trigonométricas
Taller 15 Funciones para adición y multiplicación de Ángulos
Taller 16 Ecuaciones Trigonométricas

Gracias.

Angulos de elevacion y depresion

ÁNGULO DE ELEVACIÓN: Es el ángulo que se forma entre la visual de un observador que mira hacia arriba y la horizontal
ÁNGULO DE DEPRESIÓN : Es el ángulo que se forma entre la visual de un observador que mira hacia abajo y la horizontal
ver dibujos.

Como se puede observar, en el dibujo de la izquierda, el ave observa hacia abajo al insecto y la horizontal esta a la altura de su vista, por lo tanto el angulo es de depresión. En el dibujo de la derecha el señor, sentado en su silla de ruedas, observa los globos "hacia arriba" por lo tanto el angulo es de elevación.

Para tener en cuenta: En ambos ángulos, la visual del observador será la hipotenusa del triángulo que se forma al plantear una situación problema de este tipo.

Ahora usted esta en capacidad de construir un dibujo con cada situación, diferentes a las presentadas arriba.

Ejemplos de aplicación:

NOTA. En la resolución de triángulos rectángulos vinos qué funciones y procesos utilizar de acuerdo a la información suministrada para su solución. En este tema se aplica la misma situación para resolver los interrogantes.

Ejemplo No 1

Un piloto de un barco observa al vigía de un faro con un ángulo de elevación de 32º. Si la altura del faro es de 135 m, calcular la distancia del faro al barco, y la visual del piloto.

(Una observación muy válida: si fuera el vigilante del faro el que observara al piloto del barco, entonces hablaríamos de angulo de depresión)

Solución.

Observemos la figura.

Se ha generado un triangulo rectángulo, recto en la base del faro. La visual del piloto es la hipotenusa, el ángulo de elevación está formado con la hipotenusa y la horizontal, Luego podemos construir un triangulo auxiliar donde ubicaremos a información suministrada, o si lo prefiere en el mismo dibujo.

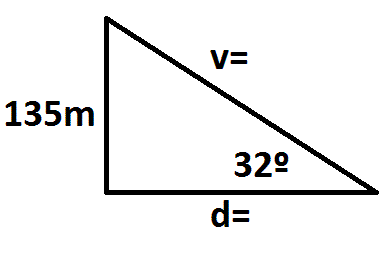
Hallamos d con la función tangente, ya que conocemos el cateto opuesto al ángulo de 32º y vamos a buscar el cateto adyacente

Ahora calculamos la visual v (hipotenusa) con la función Seno de 32º

Ambos resultados, al trabajarlos directamente en la calculadora científica, ofrecen un poco de diferencia en los decimales.
Ejemplo 2.
Un electricista subido en un poste, observa a su ayudante que está en el piso a 25 metros del pie del poste, con un ángulo de depresión de 40º. Calcular la altura del poste.
Solución. Nótese cómo se elabora la gráfica cuando se trata de ángulo de depresión, el cual aparece fuera del triángulo que que se genera, pero es igual al otro ángulo alterno interno
La información se muestra en la gráfica.

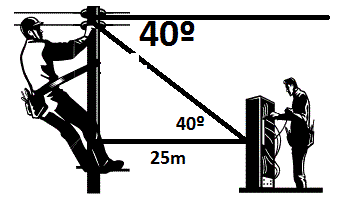
Observemos que el ángulo de depresión se trasladó al interior del triangulo
NOTA: Vemos así que el ángulo de elevación, siempre es igual al ángulo de depresión, y la visual es la hipotenusa.
Calculamos con tangente de 40º la altura h del poste.

Usted está en capacidad de hallar la medida de la visual (v), es decir, de la hipotenusa. Por favor use la función Coseno de 50º (La respuesta es 32,76 m)

EJERCICIOS
Recuerden que uno de los indicadores de desempeño es: Formular, resolver y argumentar problemas .
Favor mostrar en su, cuaderno, el proceso para llegar a la respuesta correspondiente en cada ejercicio.
1. El piloto de un avión observa a un hombre en la calle de una ciudad con un ángulo de depresión de 42°, como se muestra en la figura:

Pregunta 1: Si la visual del piloto es de 15.95 km, la horizontal del piloto en ese momento es:
A. 9.52 km
B. 8.77 km
C. 11.85m
D. 11.85 km
Pregunta 2: La altura h del piloto es aproximadamente:
A. 12.85 km
B. 10.67 km
C. 19.67 km
D. 11.93 km
Ejercicio 2. Un navegante ubica (fondea) su barco a 50 m del pie de un faro y observa la torre de éste con un ángulo de elevación de 53°, (ver figura)

Pregunta 3. La altura aproximada del faro:
A. 66,35 m
B. 26, 95 m
C. 16,35 m
D. 12.35 m
Pregunta 4: La longitud aproximada de la visual del barquero es:
A. 90,19 m
B. 83,08 m
C. 53,19 m
D. 24,83 m

lunes, 9 de noviembre de 2015

Razones trigonométricas: teorema de pitágoras y funciones trigonométricas

TEOREMA DE PITÁGORAS

Ahora bien, para empezar a estudiar las Funciones Trigonométricas, es necesario dominar lo que en Matemáticas se conoce como el Teorema de Pitágoras, para ello, nos familiarizaremos con algunos de sus términos descritos a continuación:

“En un Triángulo Rectángulo el Cuadrado de la Hipotenusa es igual a la suma de los Cuadrados de sus Catetos”

Simbólicamente se describe así:

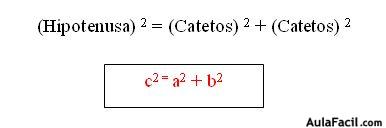
Los lados Adyacentes en un Triángulo Rectángulo se denominan Catetos, y el Lado Opuesto al Ángulo recto se llama Hipotenusa.

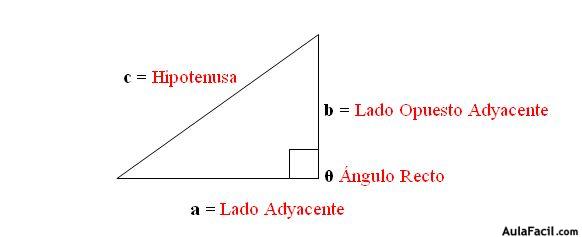
El Teorema de Pitágoras en sí, lo utilizamos para encontrar variables desconocidas, y éstas pueden ser los Lados Adyacentes o bien, la Hipotenusa.

Empecemos a trabajar con un ejemplo sencillo:

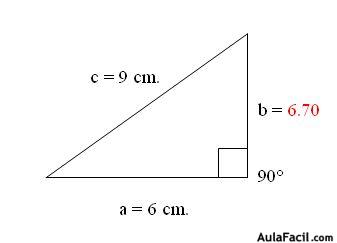
1. Se tienen los lados de un Triángulo Rectángulo a = 6 cm. y b = 6.7 cm, lado c = 9 cm.

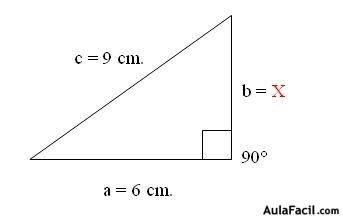
Cómo nos damos cuenta, tenemos una incógnita que debemos encontrar el valor, ésta será nuestra variable X. Aplicando el Teorema de Pitágoras, procedemos a utilizar la Fórmula:

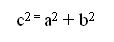
1. Empezamos por sustituir las cantidades numéricas en las variables correspondientes

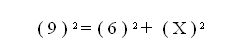
2. Realizamos las operaciones:

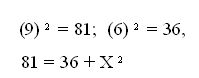
3. Procedemos a despejar la Ecuación, a modo de dejar sola la variable que queremos encontrar:

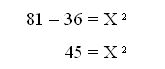
4. Para dejar la Variable sola, pasamos el exponente al otro lado, convirtiéndolo en Radical.

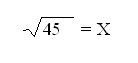
Obtenemos Raíz Cuadrada de 45 dándonos como respuesta 6.70 = X = b

FUNCIONES TRIGONOMETRICAS

Para las Funciones Trigonométricas, como se mencionó anteriormente, haremos uso del Teorema de Pitágoras y trabajaremos con las Funciones de Seno, Coseno y Tangente, y sus inversas, además de apoyarnos siempre con la Calculadora.

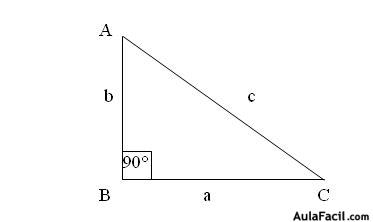
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras, las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los Ángulos del Triángulo.

Empezaremos a ver cada una de las Funciones:

1. Función Seno ( Sen): La Función Seno nos describe la relación existente entre Lado Opuesto sobre la Hipotenusa. Su simbología es la siguiente:

2. Función Coseno ( Cos): La Función Coseno describe la relación entre Lado Adyacente sobre Hipotenusa. Su simbología es la siguiente:

3. Función Tangente ( Tan): Ésta Función nos representa la relación entre Lado adyacente sobre Hipotenusa. Su simbología es la siguiente:

También tenemos las Funciones que son inversas a las anteriores:

4. Función Cotangente ( Cot): Que describe la relación entre Lado Adyacente con Lado Opuesto:

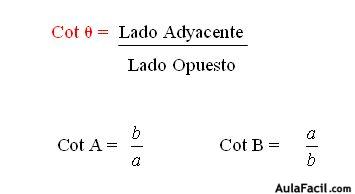
5. Función Secante ( Sec): Relación entre Hipotenusa sobre Lado Adyacente:

6. Función Cosecante ( CsC): Nos muestra la relación entre Hipotenusa sobre Lado Opuesto:

Teorema o ley del coseno

En un triángulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto del producto de ambos por el coseno del ángulo que forman.

Ejemplos

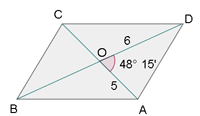
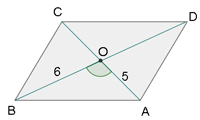
Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.

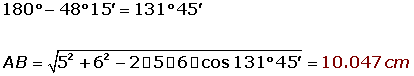
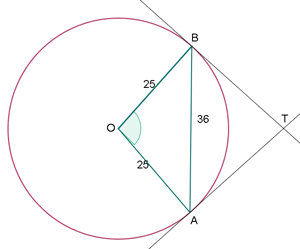
El radio de una circunferencia mide 25 m. Calcula el ángulo que formarán las tangentes a dicha circunferencia, trazadas por los extremos de una cuerda de longitud 36 m.

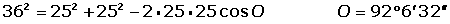
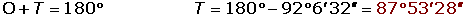
Teorema o ley del seno

Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.

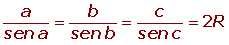
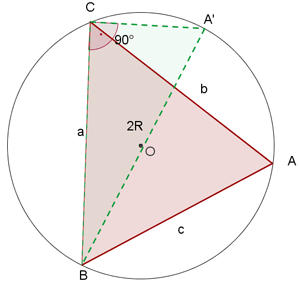
Ejercicios

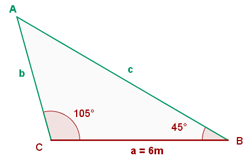
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Determina los restantes elementos.

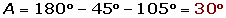
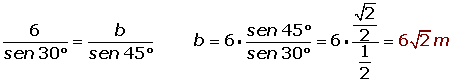
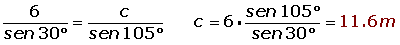
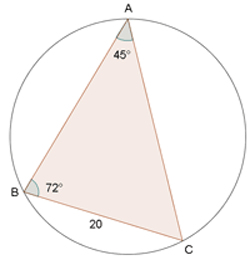
Hallar el radio del círculo circunscrito en un triángulo, donde A = 45°, B = 72° y a=20m.

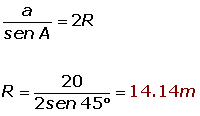
Sistema de Medidas Angulares

Son tres los Sistema de Medidas Angulares:

Sistema Sexagesimal: Se considera a la circunferencia dividida en 360 partes iguales. Cada grado se considera dividida en 60 partes iguales llamadas minutos y cada minuto en 60 partes iguales llamadas segundos.

1° equivale a 60´
1´ equivale a 60"
1° equivale a 3600"

Sistema Centesimal: Es la circunferencia dividida en 400 partes iguales, llamadas "grados centesimales". Cada grado tiene 100 "minutos centesimales" y cada minuto tiene 100 "segundos centesimales".

1g equivale a 100m
1m equivale a 100s
1g equivale a 10000s

Sistema circular: En este sistema se usa como unidad el ángulo llamado "radián". Un radián es el ángulo cuyos lados comprenden un arco cuya longitud es igual al radio de la circunferencia.

Como la longitud de una circunferencia es 2 radianes, es decir 6.28 radianes, dándole a el valor de 3.14

Un radián equivale a 57°18' (se obtiene dividiendo 360° entre 2)
EQUIVALENCIAS ENTRE LOS SISTEMAS

S/360 = C/400 = R/2

Otros casos: