Operaciones básicas de monomios y polinomios.

Suma de monomios

Sólo podemos sumar monomios semejantes.

La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.

axn + bxn= (a + b)xn

Ejemplo: 2x2y3z + 3x2y3z = (2 + 3)x2y3z = 5x2y3z

Si los monomios no son semejantes, al sumarlos, se obtiene un polinomio.

Ejemplo:

2x2y3 + 3x2y3z

Resta de un monomio con un polinomio:

Aquí se complica un poco la cosa, pero aún así es fácil, nada más tenéis que agrupar ese monomio que tenemos con la parte del polinomio que sea semejante, es decir, que tenga dentro de ese polinomio un monomio semejante al de inicio.

Digamos que tenemos esto:

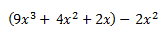
Producto de un número por un monomio

El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente del monomio por el número.

Ejemplo:

5 · (2x2y3z) = 10x2y3z

Multiplicación de monomios

La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tengan la misma base, es decir, sumando los exponentes.

axn · bxm = (a · b)xn + m

Ejemplo:

(5x2y3z) · (2y2z2) = (2 · 5) x2y3+2z1+2 = 10x2y5z3

División de monomios

Sólo se pueden dividir monomios cuando:

1. Tienen la misma parte literal

2. El grado del dividendo es mayor o igual que el el divisor

La división de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene dividiendo las potencias que tengan la misma base, es decir, restando los exponentes.

axn : bxm = (a : b)xn − m

Ejemplo División

Si el grado del divisor es mayor, obtenemos una fracción algebraica.

Ejemplo División

Potencia de un monomio  

Para realizar la potencia de un monomio se eleva, cada elemento de este, al exponente que indique la potencia.

(axn)m = am · xn · m

Ejemplos:

(2x3)3 = 23 · (x3)3= 8x9

(−3x2)3 = (−3)3 · (x2)3= −27x6

Bibliográfia  http://www.vitutor.com/ab/p/a_3.html