TALLER EXPRESIONES ALGEBRAICAS MONOMIOS

Para aquellos que entienden que esto es de práctica dejamos un taller en esta pagina que a nuestro parecer es buenisima para que puedan hacer algunos ejercicios en su tiempo libre esperamos les sirva.


Talleres

Producto notable

A continuación añadimos un breve vídeo esperamos les sea útil...

Si tienen alguna duda por favor dejen sus comentarios y con el mayor de los gustos postearemos algo que aclare sus dudas.

https://www.youtube.com/watch?v=NbWQw-qlJ_Q

Operaciones básicas de monomios y polinomios.

Suma de monomios

Sólo podemos sumar monomios semejantes.

La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.

axn + bxn= (a + b)xn

Ejemplo: 2x2y3z + 3x2y3z = (2 + 3)x2y3z = 5x2y3z

Si los monomios no son semejantes, al sumarlos, se obtiene un polinomio.

Ejemplo:

2x2y3 + 3x2y3z

Resta de un monomio con un polinomio:

Aquí se complica un poco la cosa, pero aún así es fácil, nada más tenéis que agrupar ese monomio que tenemos con la parte del polinomio que sea semejante, es decir, que tenga dentro de ese polinomio un monomio semejante al de inicio.

Digamos que tenemos esto:

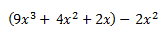
Producto de un número por un monomio

El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente del monomio por el número.

Ejemplo:

5 · (2x2y3z) = 10x2y3z

Multiplicación de monomios

La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tengan la misma base, es decir, sumando los exponentes.

axn · bxm = (a · b)xn + m

Ejemplo:

(5x2y3z) · (2y2z2) = (2 · 5) x2y3+2z1+2 = 10x2y5z3

División de monomios

Sólo se pueden dividir monomios cuando:

1. Tienen la misma parte literal

2. El grado del dividendo es mayor o igual que el el divisor

La división de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene dividiendo las potencias que tengan la misma base, es decir, restando los exponentes.

axn : bxm = (a : b)xn − m

Ejemplo División

Si el grado del divisor es mayor, obtenemos una fracción algebraica.

Ejemplo División

Potencia de un monomio  

Para realizar la potencia de un monomio se eleva, cada elemento de este, al exponente que indique la potencia.

(axn)m = am · xn · m

Ejemplos:

(2x3)3 = 23 · (x3)3= 8x9

(−3x2)3 = (−3)3 · (x2)3= −27x6

Bibliográfia  http://www.vitutor.com/ab/p/a_3.html

Casos de Factorizacion

CASOS DE FACTORIZACION

FACTORIZACION

Es una técnica que consiste en la descripción de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc.) en forma de producto.

Existen diferentes métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que recibe el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles. 

FACTORES

Se llama factores o divisores de una expresión algebraica a las expresiones algebraicas que multiplicadas entre si dan como producto la primera expresión.

Ejemplo:                 
a(a + b) = a² + ab
(x + 2) (x +3) = x² + 5x + 6
(m + n) (m- n) = m²  - mn - n² 

CASOS DE FACTORIZACION

CASO I

CUANDO TODOS LOS TERMINOS DE UN POLINOMIO TIENEN UN FACTOR COMUN

Factor Común Monomio:

Ejemplo 1:

14x² y²  - 28x³ + 56x⁴

R: 14x²  (y²  - 2x + 4x²)           

Ejemplo 2:

X³ + x⁵ – x⁷     =     R:  x³ (1 + x²  - x⁴)         

Ejemplo 3:

100a² b³c –150ab²c²  + 50 ab³c³ - 200abc²= 

R:  50abc (2ab² – 3bc  +b²c² – 4c)       

 

Factor Común Polinomio:

 

Ejemplo 1:

a(x + 1) + b(x + 1)

R:  (x + 1) (a +b)

Ejemplo 2:

(3x + 2) (x + y – z) – (3x + 2) -  (x + y – 1)( 3x +2)

 

 

R: (3x + 2) (x + y – z) – (3x + 2)(1) – ( x - y +1)( 3x +2)

 

 

     (3x + 2) (x + y – z -1 –x - y + 1)

 

     -z ( 3x +2)

Ejemplo 3:

(a + b -1) (a ² + 1) – a² – 1

R: ( a + b -1) (a ² + 1) –( a² + 1)

     ( a² + 1)(a + b - 1)-1

     ( a² + 1)(a + b  -1 -1)

      ( a² + 1)(a + b  -2)

CASO II

FACTOR COMUN POR AGRUPACION DE TERMINO

Ejemplo 1:

a² + ab + ax + bx

(a² + ab)  +  (ax + b)

a(a + b) + x(a +b)

(a + b) (a +x)

Ejemplo 2:

4am³ – 12 amn – m²  + 3n

= (4am³ – 12amn) – (m² +  3n)

=4am (m² – 3n) – (m² + 3n)

R: (m² – 3n)(4am-1)

Ejemplo 3:

a²b³ – n⁴ + a²b³x² – n⁴x² – 3a³b³x + 3n⁴x

= (a²b³ – n⁴ + a²b³x² – n⁴x² – 3a³b³x + 3n⁴x)

= (a²b³ + a²b³x²  – 3a²b³x) – (n4 + n⁴x² - 3n⁴x)

= a²b³ (1 + x² – 3x)- n⁴ (1 + x² -3x)

R:   (1 + x² – 3x) (a²b³ -  n⁴ )

 

 

CASO III

TRINOMIO CUADRADO PERFECTO

Ejemplo 1;

a² – 2ab + b²

Raíz cuadrada  de a²  = a

Raíz cuadrada  de b²   = b

Doble producto sus raíces

(2 X a  X b) 2ab  (cumple)   

R: (a – b) ²

Ejemplo 2:

49m ⁶– 70 am³n² + 25 a²n⁴

Raíz cuadrada  de 49m⁶  = 7m³  

Raíz cuadrada  de 25a²n⁴  = 5an²

Doble producto sus raíces

(2 X 7m³  X  5a²n²) =  70am³ n²  (cumple)   

R: (7m – 5an²)

Ejemplo 3:

9b² – 30 ab + 25a²

Raíz cuadrada  de 9b²  = 3b  

Raíz cuadrada  de 25 a²= 5a

Doble producto sus raíces

(2 X 3b  X  5a) =  30ab  (cumple)  

R: (3b - 5a) ²

 

 

 

CASO ESPECIAL

 

Ejemplo 1:

 

 

a² + 2a (a – b) + (a – b) ²

 

Raíz cuadrada  de a²  = a  

 

Raíz cuadrada  de (a – b) ² = (a – b)

 

Doble producto sus raíces

 

(2 X a  X  (a – b) =  2a(a – b) (cumple)   

 

R: (a + (a – b)) ²

 

    (a + a – b) = (2a –b) ²   

 

 

 

Ejemplo 2: 

(x + y) ² – 2(x+ y)(a + x) + (a + x) ²

 

Raíz cuadrada  de (x + y)²  =(x + y)  

 

Raíz cuadrada  de (a + x) ² = (a + x)

 

Doble producto sus raíces

 

(2 X (x + y)  X  (a + x)) =  2(x +y)(a + x) (cumple)   

 

R: ((x +y) – (a + x)) ²

 

    (x + y – a – x) ² = (y – a) ²

 

CASO IV

DIFERENCIA DE CUADRADOS PERFECTOS 

Ejemplo 1:

X² - y ²

x      y  = Raíces 

Se multiplica la suma por la diferencia

                R: = (x + y) (x- y) 

 

Ejemplo 2:

 

100m²n⁴ - 169y⁶

10mn²           13y³ =  Raíces

Se multiplica la suma por la diferencia    

                           R: = (10mn² + 13y³) (10mn²- 13y³)

 

Ejemplo 3:

 

1 - 9a²b⁴c⁶d⁸

1       3 ab²c³d⁴    =  Raíces

Se multiplica la suma por la diferencia     

                           R: = (1 + 3 ab²c³d⁴) (1- 3 ab²c³d⁴)

 

CASO ESPECIAL

Ejemplo 1:

(a - 2b)² - (x +  y)²

  (a - 2b)      (x + y)   = Raíces 

Se multiplica la suma por la diferencia

 

          R: = ((a - 2b) + (x + y))  ((a - b) -  (x + y))

                  (a - 2b + x + y)   (a -2b - x - y)

 

Ejemplo 2: 

16a¹⁰ - (2a² + 3) ²

4a⁵         (2a² + 3)  =  Raíces

Se multiplica la suma por la diferencia

                                    R: = ((4a⁵ + (2a² + 3))( 4a⁵ - (2a² + 3))

                                   (4a⁵ + 2a² + 3)(4a⁵ - 2a² - 3)

 

Ejemplo 3:

 

36(m + n)² - 121(m - n)²

6(m + n)           11(m - n)   =  Raíces

Se multiplica la suma por la diferencia      

                           R: = ((6(m + n) + 11(m - n)) (6(m + n) - 11(m - n))

                                  (6m + 6n + 11m -11n) (6m +6n - 11m + 11n)

                                  (17m + 5n ) (5m +17n)

 

CASOS ESPECIALES

COMBINACION DE LOS CASOS III Y IV

Ejemplo 1:

 

 

 

 

 

 

 

a² + 2ab + b² - x²

(a² + 2ab + b²) - x²

(a + b) ² - x²

 

R : (a + b + x)(a + b - x)

 

Ejemplo 2:

 

1 - a² + 2ax - x²

1 - (a² + 2ax - x²⁾

1 - (a - x)²

 

R: (1 - a + x) (1 + a + x)

 

Ejemplo 3: 

16a² - 1 - 10m + 9x² - 24ax - 25m²

(16a² -24ax +  9x²) - (1 + 10m + 25m²)

(4a - 3x) ² - (1 + 5m) ²

 

R: (4a - 3x + 5m +1)(4a -3x -5m - 1)

CASO V

 

TRINOMIO CUADRADO PERFECTO POR ADICION Y SUSTRACCION

 

Ejemplo 1:

 

a⁴ +    a² + 1

    +    a²       - a²

a⁴ + 2a²+ 1 - a²

(a⁴ + 2a²+ 1) - a²

(a² + 1)² - a²

 

R: (a²+ a + 1) (a²– a + 1)

 

Ejemplo 2: 

25⁴ + 54a²b² + 49b⁴

       + 16 a²b²             - 16 a²b²­

25⁴ + 70a²b² + 49b⁴ - 16 a²b²­

(25⁴ + 70a²b² + 49b⁴) - 16 a²b²­

(5a² + 7b)²- 16 a²b²

 

R: (5a² + 7b² + 16 ab) (5a² + 7b2- 16 ab)

     (5a² + 16ab +7b²) (5a² - 16 ab +7b²)

 

Ejemplo 3:

 

81a⁴b⁸ - 292a²b⁴x⁸ + 256x¹⁶

              +     4 a²b⁴x⁸                  – 4 a²b⁴x⁸

81a⁴b⁸ - 288a²b⁴x⁸ + 256x¹⁶  – 4 a²b⁴x⁸

(81a⁴b⁸ - 288a²b⁴x⁸ + 256x¹⁶)  – 4 a²b⁴x⁸

(9a²b⁴ - 16x⁸)²  – 4 a²b⁴x⁸

 

R: (9a²b⁴ - 16x⁸ + 2 ab²x⁴)  (9a²b⁴ - 16x⁸ –  2 ab²x⁴)

    (9a²b⁴ + 2 ab²x⁴- 16x⁸)  (9a²b⁴ –  2 ab²x⁴ - 16x⁸  )

CASO ESPECIAL

FACTORAR UNA SUMA DE DOS CUADRADOS

Ejemplo 1:

x⁴+ 64y⁴

x⁴                            + 64y⁴
      + 16x²y²                  - 16x²y²      
x⁴   + 16x²y²  + 64y⁴     - 16x²y²

(x⁴   + 16x²y²  + 64y⁴)   - 16x²y²

(x²   +  8y²)²   - 16x²y²

 

R: (x²   +  8y² + 4xy)  (x²   +  8y² - 4xy)

    (x²   + 4xy +  8y²)  (x²   - 4xy +  8y²)

 

Ejemplo 2:

 

4m⁴ + 81n⁴

4m⁴                     + 81n⁴

            + 36m²n²                 - 36m²n²
4m⁴  + 36m²n²  + 81n⁴   - 36m²n²

(4m⁴  + 36m²n² +81n⁴)   - 36m²n²

(2m² + 9n²)² - 6m²n²

 

R: (2m² + 9n² - 6mn) (2m² + 9n² - 36mn)

     (2m² + 6mn + 9n²) (2m²  - 6mn + 9n²)

Ejemplo 3: 

81a⁴ + 64b⁴

81a⁴                   + 64b⁴

          +144a²b²              - 144a²b²
81a⁴  +144 a²b² +64b⁴ -144 a²b²

(81a⁴  +144 a²b² +64b⁴) -144 a²b²

(9a² + 8b²)² - 144 a²b²

 

R: (9a² + 8b² - 12 ab) (9a² + 8b² - 12 ab)

     (9a² + 12 ab + 8b²) (9a² - 12 ab + 8b²)

CASO VI

TRINOMIO DE LA FORMA

                                                          x² + bx + c

Ejemplo 1:

x² + 7x + 10

 

R :( x + 5 )  ( x + 2 )

 

Ejemplo 2:

 

n² + 6n – 16  

R: ( n  +  8 )  ( n – 2 )

 

Ejemplo 3:

 

a² + 42a + 432

R: ( a + 24   )   (a   + 18  )

CASOS ESPECIALES

Ejemplo 1

X⁸ – 2x⁴ – 80

R: ( x⁴  – 10  )   (  x⁴   +  8  )

 

Ejemplo 2:

 

(m – n)² + 5(m – n) – 24 
 
R: (( m – n) +   8 )   ((m – n)   –  3 )    

      ( m – n +   8 )   (m – n  –  3 )    

 

Ejemplo 3:

m² + abcm – 56a²b²c²

 
R: ( m  +   8abc  )  (m   –  7abc) 

CASO VII

TRINOMIO DE LA FORMA 

                                                   ax² + bx + c

Ejemplo 1:

 

2x² + 3x – 2

(2) 2x² +(2) 3x –(2) 2

 

= 4x² + (2) 3x – 4

 

= (2x +  4 )   (2x – 1 )

         2         x      1

R= (x  +  2)  (2x – 1)

 

Ejemplo 2:

 

16m + 15m² – 15

15m² + 16m – 15

15(15m²) +(15) 16m –(15) 15

 

= 225m² + (15) 16m – 225

= (15 m  + 25 )   ( 15 m – 9 )

               5         x        3

R= ( 3m + 5 )  ( 5m  – 3 )  

 

Ejemplo 3:

 

30x² + 13x –10  

(30) 30x2 +(30) 13x – (30) 10  

900x² + (30)13x – 300

= (30x  + 25  )   (30 x – 12 )

              5         x        6

= (6x + 5) (5x – 2)

CASOS ESPECIALES

Ejemplo 1:

6x⁴ + 5x² – 6

(6) 6x⁴ + (6)5x² – (6) 6

36x⁴ + (6)5x² – 36

= (6x² + 9 )  (6x² – 4 )

           3      x      2

 

= (2x² + 3) (3x² – 2)

 

Ejemplo 2:

 

6m² – 13am – 15a²

(6) 6m² – (6) 13am – (6)15a²

36m² – (6) 13am – 90 a²

 = (6m – 18a )   (6m  + 5a )

            6         x      1

 

=  (m – 3a )  (6m  +  5a)

 

Ejemplo 3:

 

18a² + 17 ay – 15y²

(18) 18a² + (18)17 ay – (18) 15y²

324a² + (18) 17ay – 270y²

 

= (18a + 27  )   (18a – 10 )

            9          x       2

= (2a +  3y) (9a – 5y)

CASO VIII

CUBO PERFECTO DE BINOMIOS

Ejemplo 1:

a³ + 3a² + 3a + 1

Raíz cúbica de a³ =  a
Raíz cúbica de 1   = 1
Segundo término= 3(a)²(1) = 3a²
Tercer término     = 3(a)(1)² = 3a

 

R:  (a + 1)³

Ejemplo 2:

 

64x⁹ – 125y¹² – 240x⁶y⁴ + 300x³y⁸

64x⁹ – 240x⁶y⁴ + 300x³y⁸ – 125y¹²
Raíz cúbica de 64x⁹ = 4x³
Raíz cúbica de 125y¹²  = 5y⁴
Segundo término= 3(4x³)²(5y⁴) = 240x⁶y⁴
Tercer término     = 3(4x³)(5y⁴)² = 300x³y⁸

 

R:  ( 4x³ – 5y⁴ )³

 

 Ejemplo 3:

125x¹² + 600x⁸y⁵ + 960x⁴y¹⁰ + 512y¹⁵

Raíz cúbica de 125x¹² = 5x⁴
Raíz cúbica de 512y¹⁵   =8y⁵
Segundo término= 3(5x⁴)²(8y⁵) =600x⁸y⁵
Tercer término     = 3(5x⁴)(8y⁵)² =960x⁴y¹⁰

 

R:  ( 5x⁴ + 8y⁵ )³

 

 

 

CASO IX

SUMA O DIFERENCIA DE CUBOS PERFECTOS

Ejemplo 1:
  

1 + a³  

(1 + a) (1² – 1(a) +( a)²)

R:(1 + a) (1 – a + a²)

 

Ejemplo 2:

 

x³ – 27   
(x – 3 ) ((x)² + (x)3 + (3)²)

 R: (x – 3 ) (x² + 3x + 9)

 

Ejemplo 3:

 

x⁶ – 8y¹²
(x² – 2y⁴) ((x²)² + (x²)(2y4) + (2y⁴)²)

R: (x² – 2y⁴) (x⁴ + 2x² y⁴ + 4y⁸)

 

CASOS ESPECIALES

Ejemplo 1:

1 + (x + y)³  

(1 +(x + y) (1² – 1(x + y) +(x + y)²)

 

R:(1 + x + y) (1 – (x + y) + (x + y)²)

    (1 + x + y) (1 – x – y  + x² + 2xy + y²)

 

Ejemplo 2:

(m – 2)³  + (m – 3)³  

((m – 2) + (m – 3) ((m – 2)² – ((m – 2) (m – 3) + (m – 3)²)

 

R: (m – 2+ m – 3) ((m² – 4m + 4) – ((m – 2) (m – 3)) + (m² – 6m  + 9))

    (2m – 5) (m² – 4m + 4) – (m² – 3m  – 2m + 6) + (m² – 6m  + 9))

    (2m – 5) (m² – 4m + 4– m² + 3m  + 2m – 6 + m² – 6m  + 9)

    (2m – 5) (m² – 5m +7)

 

Ejemplo 3:

 

(x – y)³ – 8

((x – y) – 2)  ((x– y)² + 2(x – y) + (2)²)

 

R: (x – y – 2) (x² – 2xy + y² + 2x– 2y + 4) 

CASO X

SUMA O DIFERENCIA DE DOS POTENCIAS IGUALES

Ejemplo 1:
 

a⁵ + 1

a⁵ + 1    =  a⁴ – a³ + a² – a + 1

 a + 1

 

Ejemplo 2: 

m⁷ – n⁷

m⁷ – n⁷    =  m⁶ + m⁵n + m⁴n² + m³n³ + m²n⁴+ mn⁵ + n⁶

 m – n  


Ejemplo 3:

 

x⁷ + 128

 
x⁷ + 128    =  x⁶ – 2x⁵ + 4x⁴ – 8x³ +16x²  – 32x + 64
  x + 2